Teoria de Galois

Esta es una teoría que une el algebra con la geometria,  tiene su caracteristica mas importante en que con el conjunto de resultados que vincula la teoria de cuerpos con la de grupos. 
(La teoría de cuerpos es una rama de la matemática  que estudia las propiedades de los cuerpos . Un cuerpo es una entidad matemática para la cual la adición, sustracción, multiplicación y división están bien definidas) 
( un grupo es una estructura algebraica que consta de un conjunto con una operación  que combina cualquier pareja de sus elementos para formar un tercer elemento. Para que se pueda calificar como un grupo, el conjunto y la operación deben satisfacer algunas condiciones llamadas axiomas de grupo, estas condiciones son: tener la propiedad asociativa, tener elemento identidad y elemento simétrico)  
Galois demostró que no había posibilidad posibilidad de hallar una respuesta general a las ecuaciones de grado 5 o mayor usando la suma, resta, multiplicación...., por lo que llegamos a la conclusión de que las ecuaciones de grado 5 solo pueden ser resueltas mediante calculo numérico, Pero también hay muchas ecuaciones de grado 5 o de grado superior, que pueden llegar a resolverse de forma correcta mediante radicales, estos serían casos particulares. Galois formuló y demostró un teorema, que se llama generalmente teorema de Galois. Dicho teorema permite la identificación de las ecuaciones antes nombradas, afirmando lo siguiente: «Si en una ecuación de polinomios la potencia mayor es correspondiente a un número primo y si también se tiene el conocimiento de dos valores de la x, los demás pueden ser obtenidos a partir de ellos por medio del uso de la adición, la sustracción, la multiplicación y la división, por lo cual la ecuación puede puede resolverse por medio de radicales.»

Para una forma no tan compleja como la que nos proporcionó el teorema expresado anteriormente, procederemos identificar las ecuaciones de grado 5 y a ecuaciones superiores a 5, que pueden resolverse por medio de radicales. Es necesario entonces encontrar un nuevo concepto, que sería el concepto de grupo, el cual es bastante complejo por lo cual vamos a intentar introducirlo de una forma sencilla.
Primeramente es necesario poner atención en la forma de ordenamiento de las letras o números, estos se denominan permutaciones. Los números 1, 2 y 3 se pueden ordenar de las formas siguientes 123, 132, 213, 231, 312 y 321. Denominamos entonces a la permutación 123 permutación identidad y consideraremos entonces un modo de formular las permutaciones de manera que nos quede un par de líneas con la identidad en la línea de arriba y la permutación correspondiente en la línea inferior. Así tenemos:

Una vez establecido lo anterior, podemos definir una una operación binaria en el conjunto de permutaciones. Tendremos en cuenta dos permutaciones de cualquier tipo:

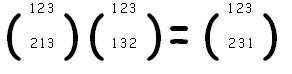
Si consideramos en primer lugar la segunda permutación y después la primera, podremos notar que lo que se ha hecho es relacionar en forma de secuencia los números que se derivan por la segunda permutación con aquellos que derivan por la primera. Esta operación. o sea este producto es interno, ya que el producto de dos permutaciones resultará en otra permutación. También se pueden verificar otras propiedades que hacen que el conjunto de las permutaciones se conforme con una estructura de Grupo en proporción a esta operación. Las propiedades son :

1. Propiedad asociativa: El ordenamiento cuando se combinan dos permutaciones contiguas no es de gran importantancia. Si denominamos a, b y c a tres permutaciones y * a la operación, la propiedad puede representarse de esta forma, (a*b)*c = a*(b*c).

2. Elemento neutro: Existe una permutación, que puede expresarse como e, de modo que cualquier permutación a, se verificará que a*e = a. En el caso estudiado la permutación neutra es la siguiente,

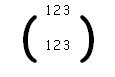
3. Elemento inverso: Dada cualquier permutación a, habrá otra, que será denotada por,

Por ejemplo, si se considera la permutación

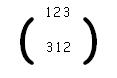
Su inversa es

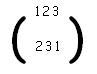
Ya que

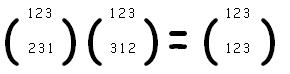
Las investigaciones de Galois han perdurado de forma puntual, llegando a formular una condición para que una ecuación de polinomios de cualquier tipo pueda determinarse mediante radicales.

Publicado por: Francisco José Ponce Parra.